Неизвестный танк часть 4 - 20

ПЕРЕДАТОЧНОЕ  ЧИСЛО ПЛАНЕТАРНОЙ  ПЕРЕДАЧИ

Определим передаточное число планетарной передачи внутреннего зацепления, у которой ведущей частью является солнечная шестерня, ведомой — водило, а венец, неподвижен.

Заменяя сателлит рычагом, мы видели, что один конец этого рычага закреплен, а другой передвигается солнечной шестерней. Очевидно, что за одно и то же время середина рычага проходит вдвое меньшее расстояние, чем его конец. Таким образом, дуга аbвдвое больше дуги cd(рис. 435); зуб сателлита  всегда движется вдвое бы­стрее, чем ось сателлита.

Рис.  435.  К определению передаточного числа планетарной передачи внутреннегозацепления

За один оборот солнечной шестерни ее зуб пройдет путь, равный длине окруж­ности солнечной шестерни. Длина этой окружности равна 2πг₁ где г₁— радиус сол­нечной шестерни. Если солнечная шестерня делает n₁об/мин, путь, пройденный ее зубом за 1 минуту, будет 2πг₁n₁ такой же путь пройдет зуб сателлита, так как его скорость в точке касания равна скорости зуба солнечной шестерни; вдвое меньший путь оси сателлита составит

2π г₁ n₁ / 2 = π г₁ n₁

Ось сателлита закреплена в водиле. За один оборот водила она описывает окружность длиной 2πг_в, где г_в - радиус водила. При п₀ об/мин водила путь, прой­денный осью сателлита за 1 минуту, будет 2π г_в п_0.

Мы рассмотрели, таким образом, путь, проходимый осью сателлита вместе с са­теллитом и вместе с водилом. Но это один и тот же путь: ось сателлита одна, она только связана с двумя разными деталями — с сателлитом и водилом; поэтому можно приравнять обе величины, написав

π г₁ п₁ = 2π г_в п₀   или, сократив на π  получим

г₁ п₁ = 2 г_в п₀

откуда

i= п₁  :  п₀  = 2г_в  :  г₁

Радиус водила равен полусумме радиусов солнечной   шестерни   и   венца, в чем легко убедиться из чертежа. Поэтому  2г_в = г₁  +  г₂,  а 

i= ( г₁  +  г₂ )  :  г₁  =  1 + г₂  : г₁

или

i= 1 + z₂: z₁

Число зубьев венца всегда больше числа зубьев солнечной шестерни, т. е. отно­шение   z2 : z1 всегда больше единицы.

Поэтому передаточное число планетарной передачи внутреннего зацепления с ведущей солнечной ше­стерней всегда больше двух, как бы мы ни изменяли число зубьев шестерен.

Когда ведущей частью является венец, а солнечная шестерня неподвижна, путь, проходимый зубом сателлита за один оборот венца, равен 2πг₂, где г₂ — радиус венца. Ось сателлита пройдет, как и в предыдущем случае, вдвое меньший путь, т. е. πг₂, а за  1  минуту при п₁  оборотах венца   πг₂п₁.

В то же время ось сателлита вместе с водилом пройдет путь, равный 2πг_вп₀  Приравнивая, как и раньше, эти две величины, найдем г₂ п₁ = 2π г_в п₀ ,  откуда

i =  n₁ :  n₀  =  2г_в  : г₂

Так как

2г_в = г₁ + г₂

 то

i= ( г₁  +  г₂ )  :  г₂  =  1 + г₁  : г₂

или

i = 1 + z₁ : z₂

Отношение   z₁: z₂   не может быть равно нулю и не может быть больше единицы.

Поэтому передаточное число планетарной пере­дачи внутреннего зацепления при ведущем венце не может быть меньше 1 и больше  2.

Таким образом, когда в планетарной передаче внутреннего зацепле­ния ведущей частью является венец, передаточные числа больше 1, но меньше 2, а когда ведет солнечная шестерня, они всегда больше 2. Этим объясняется, почему в разных случаях применяют разные передачи — либо с ведущим венцом, либо с ведущей солнечной шестерней.

Нетрудно заметить, что когда ведущей частью плане­тарной передачи внутреннего зацепления является водило, а ведомой солнечная шестер­ня, передаточное число всегда меньше 1/2. При ведущем во­диле и ведомом венце пере­даточное число планетарной передачи внутреннего зацепления всегда больше 1/2но меньше 1.

ПРЕИМУЩЕСТВА ПЛАНЕТАРНОЙ ПЕРЕДАЧИ

Допустим, что в шестеренчатой пере­даче нужно получить передаточное число i = 6. Возьмем простую пару шестерен с числом зубьев z₁= 12 ;  z₂ = 72 (рис. 436).

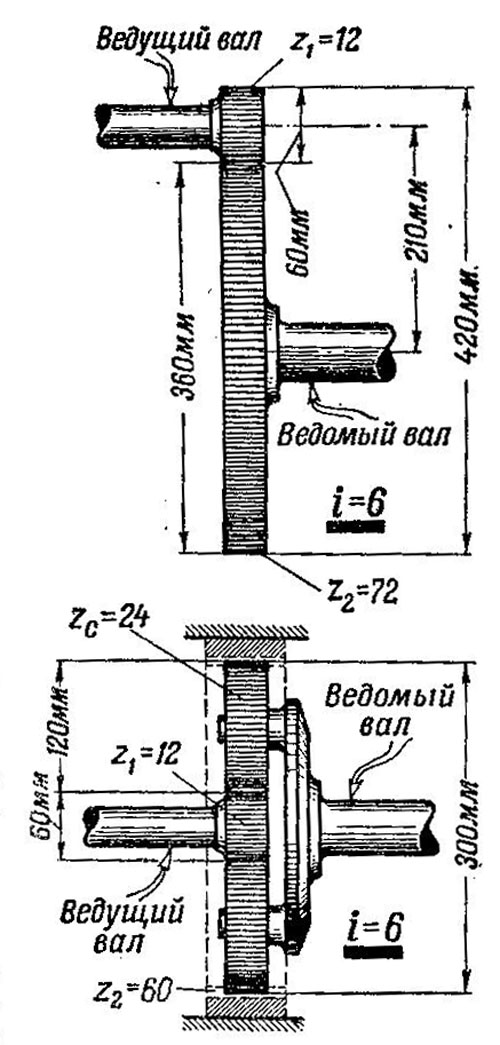
Рис. 436. Сравнительные размеры простой передачи и планетарной передачи внутреннего зацепления при одном и том же передаточ­ном числе

Пусть диаметр одной шестерни d₁= 60 мм. Тогда диаметр другой d₂= = 6 x60 = 360 мм. Наибольший размер всей передачи равен 360 + 60 = 420 мм.

В планетарной передаче внутреннего зацепления для того же передаточного числа i= 6 при z₁\ = 12 число зубьев са­теллита должно равняться  24, а числозубьев венца  z₂= 60,   так как  I= 1+60:12 = 6. Если диаметр солнечной ше­стерни d₁= 60 мм, то диаметр венца — наибольший размер всей передачи — ра­вен d₂=5d₁= 300 мм_у т. е. почти в 1,5 раза мейьше, чем у обычной непланетар­ной передачи.

Таким образом, размеры планетарной передачи внутрен него зацепления получаются значительно мень­ше, чем размеры простой шестеренчатой передачи с тем же передаточным числом. Правда, это преимущество проявляется лишь при больших передаточных числах.

Планетарные передачи имеют еще следующие преимущества. Крутя­щий момент в них передается одновременно через несколько пар зубьев, соответственно числу имеющихся сателлитов, а не через одну пару зубьев, как в обычной передаче; это позволяет уменьшить размеры зубьев шестерен, а значит, и сами ше­стерни или обеспечить большую их прочность. Для танковых передач, ра­ботающих с большими нагрузками, это особенно важно.

Ведущий и ведомый валы планетарной передачи расположены соосно, т. е. на одной прямой, что также является преимуществом плане­тарной передачи, так как дает возможность сделать механизм меньше компактнее.

Благодаря этим и некоторым другим достоинствам планетарные пе­редачи нашли широкое применение в танках, хотя по устройству они и сложнее обычных. Как мы увидим ниже, планетарная коробка передач имеет еще некоторые преимущества по сравнению с обычной шестерен­чатой коробкой передач.

• Назад
• Вперед